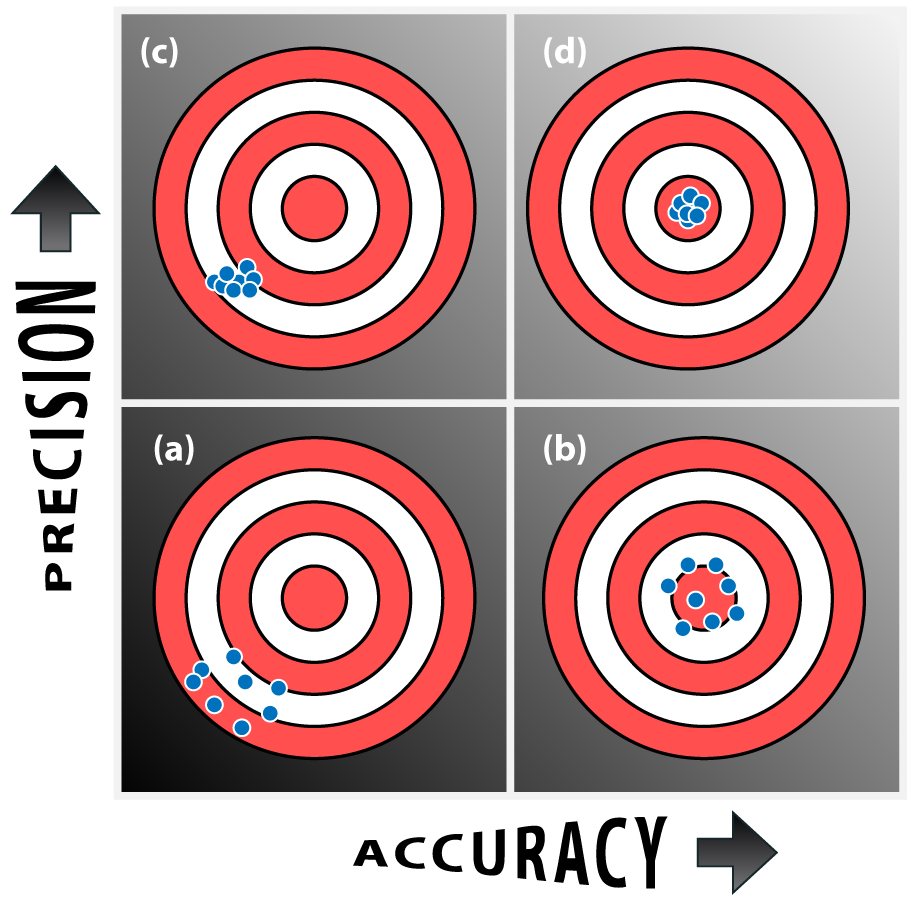
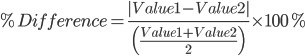Measurements and Units Accuracy, Precision, and Errors
A measurement is a quantitative observation that consists of two parts: a number and a unit. Why are units important?
| 45,000 | has little meaning – just a number |
| 45,000 dollars | has some meaning – money |
| 45,000 dollars/year | has more meaning – a person’s salary |
The SI System
Scientists realized long ago that standard systems of units had to be adopted if measurements were to be useful and they were to communicate their results. For this reason, the SI System (International System of Units - Système Internationale d’Unités) was established as the scientific system of measurement. These are some fundamental quantities in the SI system:
| Physical Quantity | Unit | Abbreviation |
|---|---|---|
| Length | meter | m |
| Mass | kilogram | kg |
| Time | second | s |
| Temperature | kelvin | K |
| Number of particles | mole | mol |
| Electric current | ampere | A |
| Luminous intensity | candela | cd |
All other physical quantities have units that can be derived from the SI base units.
e.g. velocity = displacement / Δ time - Derived SI units: m s-1
e.g. acceleration = Δ velocity / Δ time - Derived SI units: m s-2
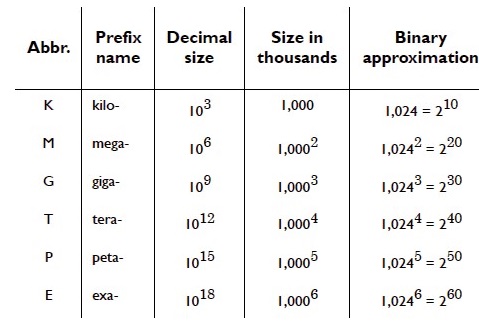
SI is a decimal system. Quantities differing from the base unit by powers of ten are noted by use of prefixes. Changing the prefix alters the size of a unit.
e.g. 1 kilometer = 1000 m. The most common SI prefixes can be found in any first year chemistry or physics textbook.
Conversion factors
It is often necessary to convert a given result from one SI unit to another (e.g. km to m). We use dimensional analysis and conversion factors to get the result in the units we want.
Consider: 1 m = 100 cm
Thus, the ratio 100cm/1 m is a conversion factor that, when multiplied by any length in meters, converts that length to centimeters.
Essentially, conversion factors are the ratio between two units.
Dimensional Analysis
It is often necessary to convert a given result from one SI unit to another (e.g. km to m). We use dimensional analysis and conversion factors to get the result in the units we want.
To convert a quantity with one set of units to a different set of units, we set up a conversion pathway by multiplying by one or more conversion factors.
EXAMPLE: Creatinine is a substance found in blood. In an analysis of a blood serum sample that detected 0.58 mg of creatinine, how many micrograms are present?
There are cases where the units of both the numerator and denominator must be converted.
EXAMPLE: A nerve impulse in the body can travel as fast as 400 feet/second. What is its speed in meters/ min? Given: 1 m = 3.3 ft.
Desired units 
Cancelling out units is a way of checking out that your calculation is set up correctly. Use the same method for more complicated situations (when units are squared, cubed, etc.).
EXAMPLE: How many square feet (ft 2) correspond to an area of 1.00 square meter (m 2 ) given that 1 m = 39.37 in and 12 in = 1 ft.?
Conversion factors can be raised to other powers.
Measuring Properties of Matter
Basically, the properties of matter can be classified into two groups: extensive and intensive properties.
Extensive properties depend on the quantity of sample observed, such as mass and volume.
Mass vs. Weight
Mass (m) is the quantity of matter in an object. The SI base unit is the kilogram (kg); however, the gram (g) is more commonly used in Chemistry. The mass of an object is fixed and independent of where or how it is measured.
Weight is the force of gravity on an object, directly proportional to mass: W ∝ m and W=mass Gravity . The weight of an object may vary because gravity varies slightly from one point on Earth to the other.
| Mass | Weight |
|---|---|
| Mass is always a constant (at any place and time) | Gravity changes and depends on gravity at the place |
| Is measured in Kilograms (SI system) | Is measured in Newtons |
| Can never be zero | Can be Zero ( with no gravity) |
| Is an intrinsic property of an object and is dependent of any external factor |
Depends on:
|
Volume
Volume is the amount of space that an object occupies. The more common non-SI unit to use is the liter (L). The most common unit used in the lab is the milliliter (mL). Recall that:
1 mL = 1 cm3 (cubic centimeter)
1 L = 1 dm3 (cubic decimeter)
Temperature
Intensive properties do not depend on the quantity of sample observed; they are characteristics of the substance itself being measured, regardless of quantity, and can be used to identify substances. Some examples of intensive properties are temperature, density, melting and boiling points.
Temperature is the measure of the thermal energy of a system. Three common scales are used: Fahrenheit (°F), Celsius/Centigrade (°C), and Kelvin (SI temperature scale). The Kelvin (K) scale assigns a value of zero to the lowest conceivable temperature, 0 K unit ( -273.15 °C).
EXAMPLE: Converting °F to °C
If the temperature outside is 20 °F, what is the temperature in °C?
EXAMPLE: Converting between Kelvin and Celsius Scales
If the temperature outside is 20.10 °C, what is the temperature in K?
Note some common temperatures:
- 0 °C = 273.15 K (often rounded off to 273 K)
- 0 K = -273.15 °C (often rounded off to -273 °C )
- 25 °C = 298.15 K (often rounded off to 298 K)
Density
Density (d) is an intensive property of a substance based on two extensive properties: mass and volume.
SI derived unit: kg/m3. More common units used in the lab are g/cm3 and g/mL
Dependence of density on temperature
Density is a function of temperature because volume varies with temperature, whereas mass remains constant.
at 4 °C
at 20 °C
EXAMPLE: What is the density of 5.00 mL of a fluid if it has a mass of 5.23 g?
EXAMPLE: What would be the mass of 1.00 L of this sample?
m= V × d
Accuracy vs. precision
Accuracy and precision are terms often used to describe the reliability of measurements. However, they must be clearly differentiated. Accuracy refers to how close a measured value is to the real or “true” value. Precision refers to the degree of reproducibility of a measured quantity (the closeness of agreement when the same quantity is measured several times–how close the measurements are to each other). This difference is demonstrated in the following illustration:
Ways of comparing experimental values
Percent error
Used to compare an unknown value with a theoretical value. It is a measure of the degree of accuracy.
Percent difference
Used to compare two experimental values which are expected to be the same. It is a measure of the degree of precision. It is also used to compare two values which are not necessarily expected to be the same. (Particularly useful to determine which are the best runs to use for calculations in titration experiments).
EXAMPLE: It is necessary to calculate the percentage difference between the best two runs (e.g the ones with the smallest % difference). In the example below, the best runs to use would be 2 & 3 since their % difference is smallest( < 1%).
| Runs | % Difference |
|---|---|
| 1 & 2 | 1.79% |
| 1 & 3 | 0.97% |
| 2 & 3 | 0.82% |
Percent change (or percent recovery)
Used to compare two values which are different due to an imposed stress on a system. It is a measure of the degree of the effect caused by the stress.
