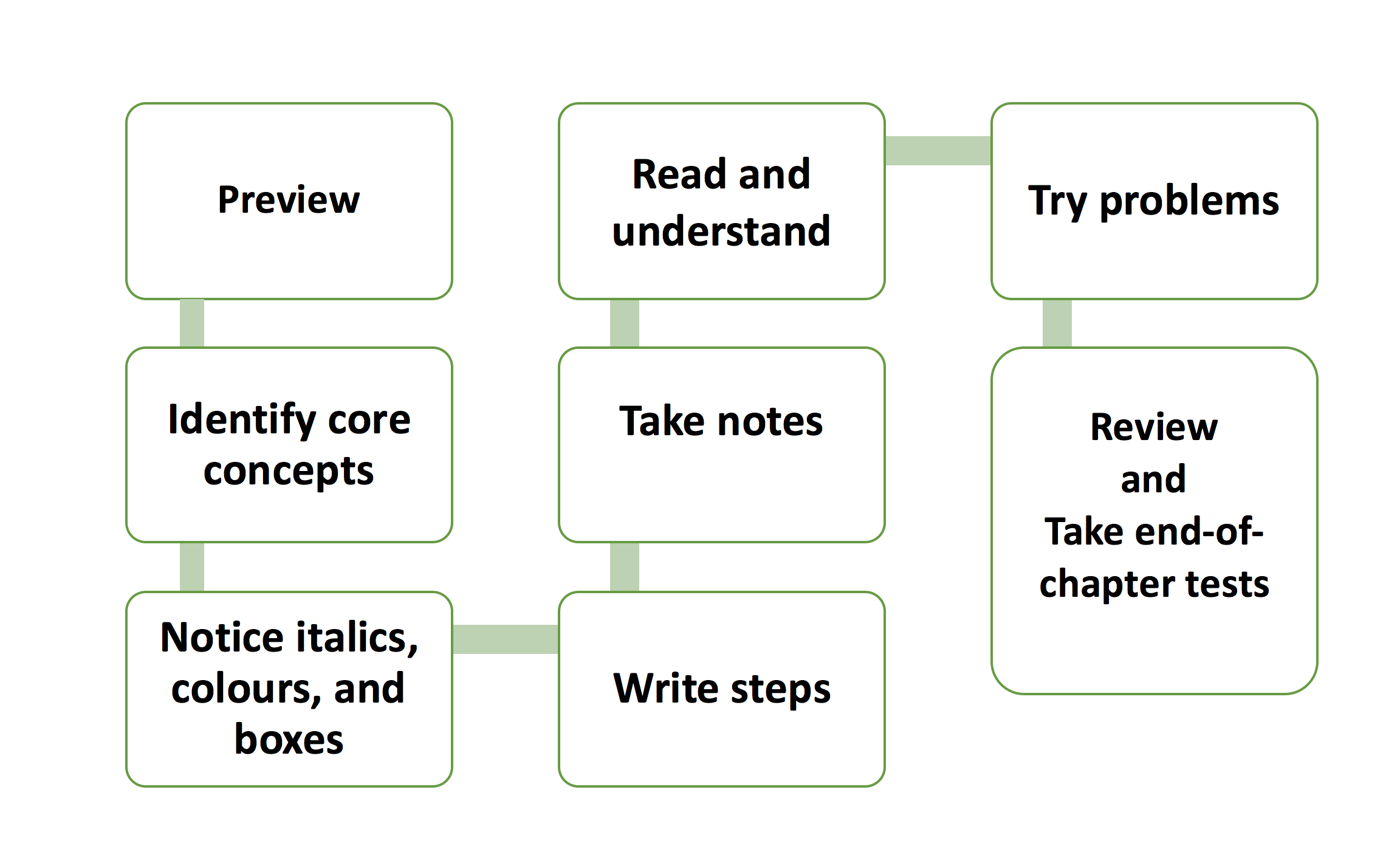
Math tests will assess your understanding of the concepts and your skill at applying these concepts. There may be multiple choice, problem solving, and calculation questions that will ask you to solve, evaluate, and calculate.

Tips and Techniques
|
1. Briefly skim through the whole test before you begin to find out what are the easiest and hardest parts so you can plan your time.
|
|
2. Identify which sections count for the most points.
|
|
3. Read the directions very carefully so that you follow the requested steps completely.
|
|
4. Being well prepared for the test is the best way to reduce anxiety.
|
|
5. Continually reviewing the class material over weeks or days is the key to success. (Don’t wait till the night before!)
|
|
6. Do the simple questions first to help you build up your confidence for the harder questions.
|
|
7. Don’t worry about how fast the other classmates finish their test. When considering exam timing, just concentrate on your own test.
|
Example sequence for taking a math test
- Calculations - they can give you the most confidence because you can check your answers and make sure that they are right.
- Problem Solving - because these questions usually count for the most marks on exams, a good strategy is to spend more time on this section.
- Multiple Choice - these questions are usually worth the least marks so spend less time on each.
Please note that this is just an example and you should rearrange this sequence based on your own preference.
Tips for calculations questions
- Step by step. Do not skip any step(s) when solving these questions. Write down all the steps you took and show all your work.
- Make a clear layout so that it will be easier to go back and check your work if you run into problems along the way solving the question.
- Check or redo calculations to make sure that your answer is right (if there is enough time). You can either do this right away or return to the calculation after finishing the rest of the exam.
Strategies for Problem Solving
- Extract relevant information/numbers from the problem, list them on your paper, and determine what they are.
e.g. principle = 200,000 dollars, year = 5 years, interest = 2.3%
- Understand what the question is asking you by highlighting, circling, or underlying key words.
e.g. what is the future value?
- Identify the formula that you need to use.
e.g. y = mx + b
Example
- Extract numbers from the problem, list them and determine what they are.
(e.g. principle = 200,000 dollar, year = 5 years, interest = 2.3% annually)
- Understand what the question is asking by highlighting, underlining, or circling key words.
(e.g. what is the future value)
- Create Cost and Revenue formulas:
| Equations: |
| X = unit of sale (production) |
| Cost formula: C(X) = variable cost × X + fixed cost |
| Revenue formula: R(X) = selling cost × X |
- With the Cost formula, find the following:
- What is the Y-Intercept? (O, Y)
- What is the X-Intercept? (X1, 0), (X2, 0)
- What is the Max/Min?
- Where does the graph start? (X, Y)
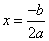
- With the Revenue formula, find the following:
- What is the Y-Intercept? (O, Y)
- What is the X-Intercept? (X1, 0), (X2, 0)
- What is the Max/Min?
- Where does the graph start? (X, Y)
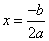
- Find your Break-Even:
(note: at Break-Even your profit is 0)
Profit = revenue - cost
(X1, Y1), (X2, Y2)
- Now you should have enough information to plot your graph.
Remember to label every single point you have found above, and also LOSS and PROFIT!